Browse Media Learn More

Free Membership - Access to more than just media

Families and school personnel (including those in training) who have at least one student with a disability can sign up for free membership.

Accessible Media

Standards-aligned videos with high-quality captions and audio description.

Teaching Tools

Create lessons and assign videos to managed Student Accounts.

Training Videos

Educator and sign language training videos for school personnel and families.
Learning Center

Find resources for providing equal access in the classroom, making media accessible, and maximizing your use of DCMP's free services.
Visit Learning Center

Accessibility Information

DCMP's Learning Center provides hundreds of articles on topics such as remote learning, transition, blindness, ASL, topic playlists, and topics for parents.

See All

Accessibility Guidelines

DCMP offers the only guidelines developed for captioning and describing educational media, used worldwide.
Captioning Key
Description Key

Help Center

Learn how to apply for membership, find and view accessible media, and use DCMP’s teaching tools.
Help Center
Continuing Education and Professional Development

DCMP offers several online courses, including many that offer RID and ACVREP credit. Courses for students are also available.
See All eLearning Resources

QuickClasses

Asynchronous, online classes for professionals working with students who are deaf, hard of hearing, blind, low vision, or deaf-blind.

See QuickClasses

Workshops

For interpreters, audio describers, parents, and educators working with students who are hard of hearing, low vision, and deaf-blind.
See Workshops

Modules

Modules are self-paced, online trainings designed for professionals, open to eLearners and full members.
See Modules

Students

These self-paced, online learning modules cover the topics of transition, note-taking, and learning about audio description.

See Student Courses
Make your educational content accessible and broadly available.

DCMP can add captions, audio description, and sign language interpretation to your educational videos and E/I programming.
Learn More

Accessibility

Captions are essential for viewers who are deaf and hard of hearing, and audio description makes visual content accessible for the blind and visually impaired.

Distribution

DCMP can ensure that your content is always accessible and always available to children with disabilities through our secure streaming platforms.

Meet our partners

DCMP partners with top creators and distributors of educational content. Take a look
About the Described and Captioned Media Program

The DCMP provides services designed to support and improve the academic achievement of students with disabilities. We partner with top educational and television content creators and distributors to make media accessible and available to these students.
Contact Us
Services

Captioning, audio description, and ASL services

Professional training for school personnel

Distribution of fully accessible streaming media

Projects

Media Center

Television Access

We Describe the World

YouTube Audio Description

Privacy and TOS

Privacy Statement

Terms of Service

Mission and Funding

Read More

Welcome to Algebra I: Simplifying Square Roots of Whole Numbers

16 minutes 18 seconds

Now Playing As: Captioned (English) (change)

In this program, students learn the basics of simplifying square roots by factoring the whole number. Part of the "Welcome to Algebra I" series.

Media Details

Runtime: 16 minutes 18 seconds

Topic: Mathematics
Subtopic: Algebra, Mathematics
Grade/Interest Level: 7 - 12
Standards:

Release Year: 2014
Producer/Distributor: PBS Learning Media
Series: Welcome to Algebra I

Course Overview Course Modules

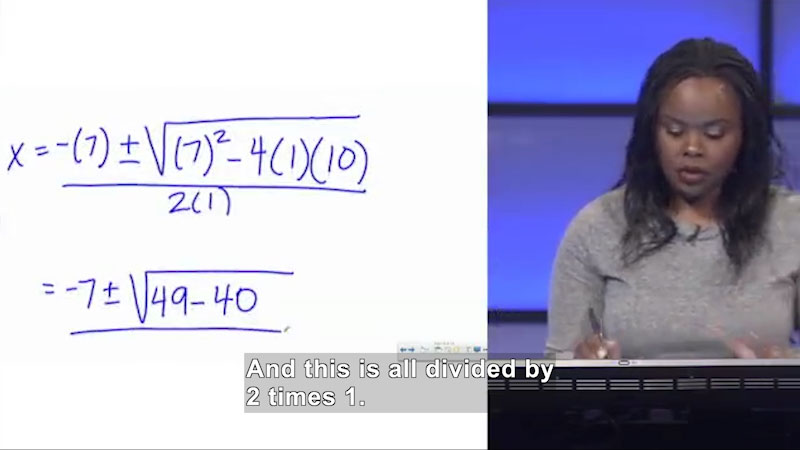
Woman with dark hair wearing a gray shirt stand at a podium in front of an illuminated blue and purple background. She holds a pen in her right hand while looking down at a screen in front of her.

Woman with dark hair in a bun wearing a green shirt stands at a podium in front of an illuminated blue and purple background. She holds a pen in her right hand while looking down at a screen in front of her.

Closeup of a large screen on top of a podium with a hand holding a pen writing numbers. Title on the screen reads, "Multiplication Property of Inequality. A equals 1, B equals 2, C equals 3." An if and then table appears below and reads, "If A is less than B and C is positive, then A, C is less than B, C."

Aerial side view of a hand using a stylus to work out a math problem on a computer screen. Text on screen reads, "Example 2. Write the numeric expression in its simplest radical form."

Split screen. The left is a white background with blue text that reads, "How did I get that?" followed by the algebra equation, 9, X, sup 5, Y minus 4, X sup 3, plus X squared. To the right, a woman works through the problem using a screen in front of her.

Split screen. The left is a white background with blue text that reads, "Example 3. The bill at the restaurant was split evenly 4 ways." Handwriting below reads, B is to Bill. To the right, a woman works through the problem using a screen in front of her.

Split screen. The left is a white background with blue text that reads, "Example 2. Evaluate 3 minus 10, X, when X equals 2 over 5." Handwriting below reads, 3 minus 10 times 2 over 5. To the right, a woman works through the problem using a screen in front of her.

Split screen. The left is a white background with a chart with 2 rows and 3 columns labeled, "Verbal, Explanation, Example." The boxes are filled in with a combination of typed and handwritten text. To the right, a woman works through the problem using a screen in front of her.

Split screen. The left is a white background with a math word problem written in blue. Text at the top reads, "Example 3. Determine if the situation presents a direct variation. Below this, the problem is in typed text and the answer is in handwritten text. To the right, a woman works through the problem using a screen in front of her.

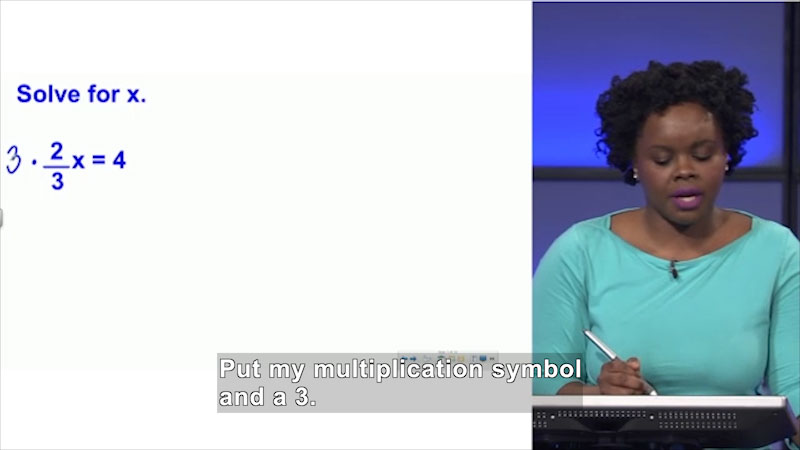
Split screen. The left is a white background with blue text that reads, "Solve for x. 3 times 2 over 3, X equals 4." To the right, a woman works through the problem using a screen in front of her. Caption. Put my multiplication symbol and a 3.