skip to main content

Welcome to Algebra I: Properties of Inequality

17 minutes 24 seconds

Now Playing As: Captioned (English) (change)

In this program, students learn about the properties of inequalities. For example, if the same amount is added to both sides of an inequality, then the inequality is still true. Part of the "Welcome to Algebra I" series.

Media Details

Runtime: 17 minutes 24 seconds

Course Overview Course Modules
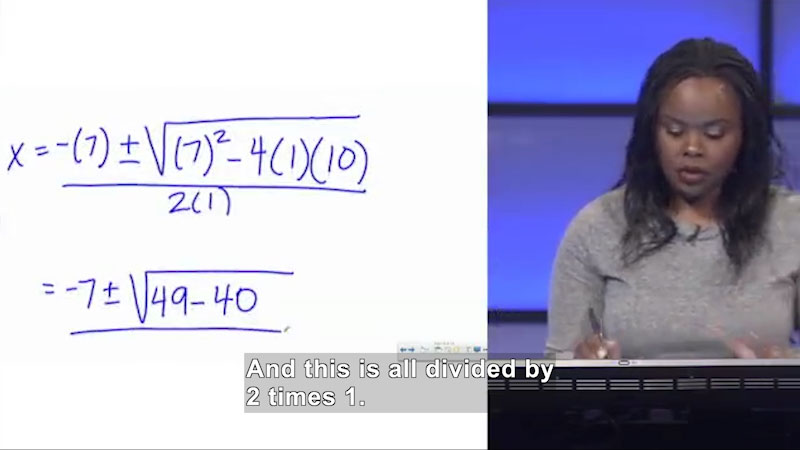
Woman with dark hair wearing a gray shirt stand at a podium in front of an illuminated blue and purple background. She holds a pen in her right hand while looking down at a screen in front of her.
Welcome to Algebra I
Episode 1
30 minutes 32 seconds
Grade Level: 7 - 12
Woman with dark hair in a bun wearing a green shirt stands at a podium in front of an illuminated blue and purple background. She holds a pen in her right hand while looking down at a screen in front of her.
Welcome to Algebra I
Episode 2
24 minutes 38 seconds
Grade Level: 7 - 12
Closeup of a large screen on top of a podium with a hand holding a pen writing numbers. Title on the screen reads, "Multiplication Property of Inequality. A equals 1, B equals 2, C equals 3." An if and then table appears below and reads, "If A is less than B and C is positive, then A, C is less than B, C."
Welcome to Algebra I
Episode 3
17 minutes 24 seconds
Grade Level: 7 - 12
Aerial side view of a hand using a stylus to work out a math problem on a computer screen. Text on screen reads, "Example 2. Write the numeric expression in its simplest radical form."
Welcome to Algebra I
Episode 4
16 minutes 18 seconds
Grade Level: 7 - 12
Split screen. The left is a white background with blue text that reads, "How did I get that?" followed by the algebra equation, 9, X, sup 5, Y minus 4, X sup 3, plus X squared. To the right, a woman works through the problem using a screen in front of her.
Welcome to Algebra I
Episode 5
21 minutes 21 seconds
Grade Level: 7 - 12
Split screen. The left is a white background with blue text that reads, "Example 3. The bill at the restaurant was split evenly 4 ways." Handwriting below reads, B is to Bill. To the right, a woman works through the problem using a screen in front of her.
Welcome to Algebra I
Episode 6
8 minutes 48 seconds
Grade Level: 7 - 12
Split screen. The left is a white background with blue text that reads, "Example 2. Evaluate 3 minus 10, X, when X equals 2 over 5." Handwriting below reads, 3 minus 10 times 2 over 5. To the right, a woman works through the problem using a screen in front of her.
Welcome to Algebra I
Episode 7
23 minutes 57 seconds
Grade Level: 7 - 12
Split screen. The left is a white background with a chart with 2 rows and 3 columns labeled, "Verbal, Explanation, Example." The boxes are filled in with a combination of typed and handwritten text. To the right, a woman works through the problem using a screen in front of her.
Welcome to Algebra I
Episode 8
14 minutes 7 seconds
Grade Level: 7 - 12
Split screen. The left is a white background with a math word problem written in blue. Text at the top reads, "Example 3. Determine if the situation presents a direct variation. Below this, the problem is in typed text and the answer is in handwritten text. To the right, a woman works through the problem using a screen in front of her.
Welcome to Algebra I
Episode 9
24 minutes 25 seconds
Grade Level: 7 - 12
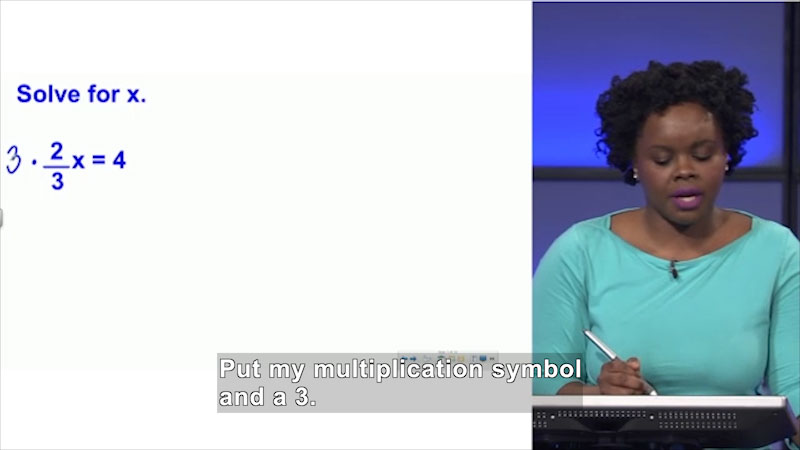
Split screen. The left is a white background with blue text that reads, "Solve for x. 3 times 2 over 3, X equals 4." To the right, a woman works through the problem using a screen in front of her. Caption. Put my multiplication symbol and a 3.
Welcome to Algebra I
Episode 10
15 minutes 43 seconds
Grade Level: 7 - 12
Apply for a Free Membership

Major funding provided by the Department of Education