Welcome to Algebra I: Solving Quadratic Equations Algebraically
"Welcome to Algebra I" focuses on solving quadratic equations algebraically, utilizing factoring techniques and the quadratic formula. The video begins with a refresher on factoring trinomials in standard form: ax^2 + bx + c, using examples to demonstrate the importance of identifying factors that satisfy both product and sum criteria. The transition is made to solving quadratic equations by recognizing these trinomials set to zero, where solutions are referred to as 'zeros' or 'roots'. The quadratic formula, shown as x = -b ± v(b^2 - 4ac) / 2a, is introduced for situations where factoring is complex. This method strengthens proficiency in math foundations as aligned with Common Core standards, enhancing problem-solving skills. Part of the "Welcome to Algebra I" series.
Media Details
Runtime: 30 minutes 32 seconds
- Topic: Language Arts, Mathematics, Social Science
- Subtopic: Algebra, Critical Thinking, Mathematics, Problem Solving
- Grade/Interest Level: 7 - 12
- Standards:
- Release Year: 2014
- Producer/Distributor: PBS Learning Media
- Series: Welcome to Algebra I
- Report a Problem
Available Resources
Related Media
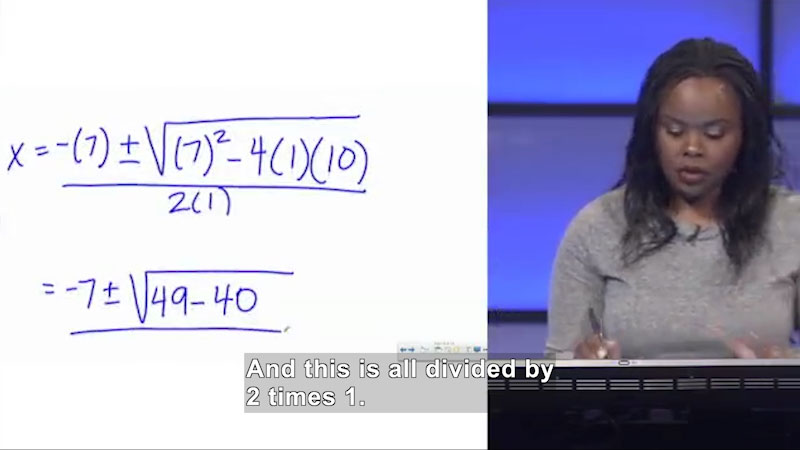
Welcome to Algebra I: Solving Quadratic Equations Algebraically

Welcome to Algebra I: Representing an Inverse Variation Algebraically

Welcome to Algebra I: Properties of Inequality

Welcome to Algebra I: Simplifying Square Roots of Whole Numbers

Welcome to Algebra I: Introduction to Polynomials

Welcome to Algebra I: Modeling Real-World Situations

Welcome to Algebra I: Evaluating Expressions

Welcome to Algebra I: Translating Expressions

Welcome to Algebra I: Determining if a Direct Variation Exists
Welcome to Algebra I: Solving Literal Equations
